✓ The Missing Probability

|

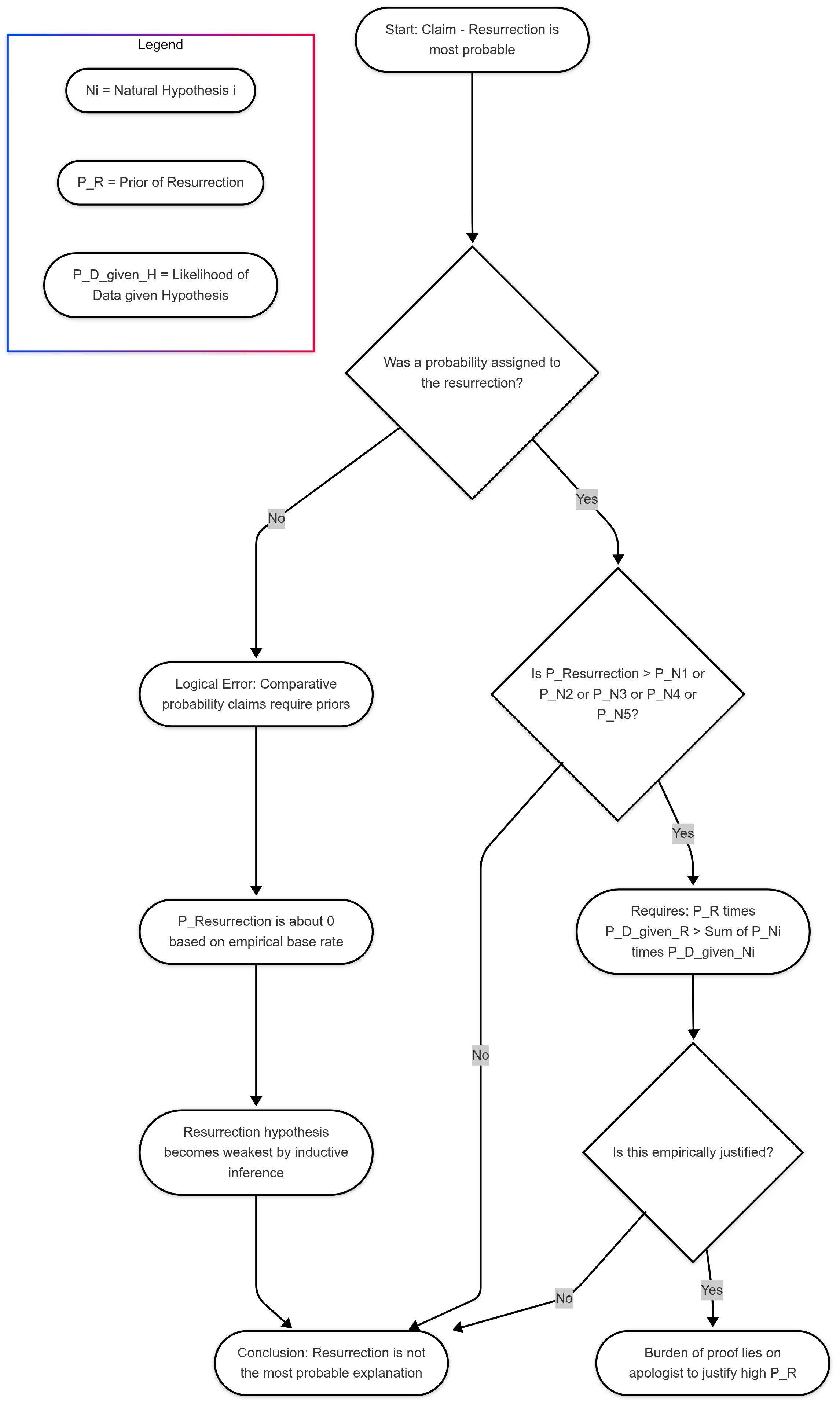
The Logical Failure of Omitting Resurrection Probability While Claiming It is “Most Probable”

One of the most foundational requirements of rational discourse—especially when adjudicating between competing explanatory hypotheses—is the assignment of relative probabilities. Without this, no comparative claim can be meaningfully asserted. Yet in Christian apologetics, it is not uncommon to encounter the claim that “the resurrection is the most probable explanation” of the empty tomb or the post-crucifixion reports—without any numerical or inferential probability being assigned to the resurrection hypothesis itself. This omission is not merely an oversight; it is a categorical violation of rational inference and epistemic responsibility. This essay will detail the logical implications of this omission and demonstrate why such claims collapse under scrutiny.

Why Probabilistic Comparison Requires All Terms

In any evaluation of competing explanations, Bayesian reasoning provides the normative standard. Bayes’ Theorem is formally represented as:

P(H \mid D) = \frac{P(D \mid H) \cdot P(H)}{P(D)}

Where:

  • P(H \mid D] is the posterior probability of the hypothesis given the data
  • P(D \mid H) is the likelihood of observing the data assuming the hypothesis is true
  • P(H) is the prior probability of the hypothesis
  • P(D) is the total probability of observing the data under all hypotheses

In the case of the resurrection, defenders often highlight anecdotal or testimonial evidence (e.g., post-crucifixion appearances, conversions, eyewitness claims) and argue that these are best explained by Jesus rising from the dead. But unless one specifies P(\text{Resurrection})—the prior probability—the formula breaks down. The comparison to other hypotheses becomes meaningless.

One cannot validly say, “H is more probable than A, B, C, D, and E” unless P(H) and P(H \mid D) are provided and shown to exceed the respective values of P(A \mid D), P(B \mid D), etc.

The Resurrection’s Incoherent Probability Default

What is the value of P(\text{Resurrection})? Given all documented human history, where the base rate of biologically dead individuals returning to life is zero, this yields:

P(\text{Resurrection}) \approx \frac{0}{\text{Observed Human History}} = 0

This does not imply metaphysical impossibility, but it does establish an empirical prior probability that is functionally infinitesimal. The apologetic strategy, however, frequently evades this issue and instead pretends the prior is unspecified or irrelevant. This is epistemically incoherent. One must address the resurrection’s base rate if one is to include it in any comparative analysis.

Disjunction of Natural Hypotheses

Consider the five most common naturalistic theories:

  1. Stolen body by disciples
  2. Stolen body by robbers
  3. Wrong tomb
  4. Apparent death (swoon theory)
  5. Never buried (body discarded or destroyed)

Suppose each is given a minimal probability of 0.1%:

P_1 = 0.001 P_2 = 0.001 P_3 = 0.001 P_4 = 0.001 P_5 = 0.001

Then the disjunction (i.e., the chance that at least one is true) is:

P(\text{At least one naturalistic explanation}) = 1 - (1 - P_1)(1 - P_2)(1 - P_3)(1 - P_4)(1 - P_5) = 1 - (0.999)^5 \approx 0.005

Even at highly conservative estimates, this value dwarfs the resurrection’s prior.

Formal Logic Summary

Let:

  • R = Resurrection hypothesis
  • N_i = Naturalistic hypotheses (for i = 1 to 5)
  • D = Data (e.g., empty tomb, post-crucifixion appearances)

Then the apologetic claim is:

P(R \mid D) > P(N_1 \mid D) \vee P(N_2 \mid D) \vee \dots \vee P(N_5 \mid D)

But without assigning a value to P(R), this statement is void. In fact, using Bayesian calculus:

P(R \mid D) = \frac{P(D \mid R) \cdot P(R)}{P(D)} P(N_i \mid D) = \frac{P(D \mid N_i) \cdot P(N_i)}{P(D)}

So the comparison depends entirely on the ratio:

\frac{P(D \mid R) \cdot P(R)}{P(D \mid N_i) \cdot P(N_i)}

Without specifying P(R), the apologist is making an invalid comparative assertion.

Conclusion: Neglecting Resurrection Probability Invalidates the Claim

In summary:

  • The claim that “the resurrection is the most probable explanation” requires a quantified or at least reasoned P(\text{Resurrection}).
  • This requirement is consistently ignored or evaded in apologetic arguments.
  • Since the base rate of resurrections is effectively zero, any minimally probable natural theory will, in sum or individually, exceed the resurrection in probability.
  • Therefore, the failure to provide a resurrection probability is not a minor lapse—it is a logical disqualification from making any comparative claim of probability.

Until the resurrection hypothesis is given a coherent probability assignment, any argument that it is “most probable” must be dismissed as epistemically incoherent and logically invalid.

2 responses to “✓ The Missing Probability”

  1. Steve H Avatar
    Steve H

    Phil, my understanding of the Bayesian analysis of Jesus’ resurrection is based on the Odds Form of Bayes’ Theorem. That form incorporates both the Prior Probabilities (ie. background evidence; knowledge of natural vs supernatural causes) and the Likelihood Probabilities (ie. likelihood of the truth vs falsity of the claim/hypothesis/resurrection in light of having vs not having evidence of empty tomb, post-mortem appearances, origin of disciples’ beliefs).

    That is, the Likelihood Probabilities (LP) calculation can far outweigh the Prior Probabilities (PP) calculation given the existence of evidence which would not otherwise exist if the claim were false. More specifically, the denominator of the LP (probability of existence of evidence if claim is false) is extremely small compared to the LP numerator (probability of existence of evidence if claim is true), which results in a very large LP calculation, which in turn can outweigh the PP.

    Thus, extraordinary claims, if true, require a higher probability of *ordinary* evidence, which can support the resurrection hypothesis as the best explanation over natural hypotheses.

    Your thoughts?

    Reply
  2. Phil Stilwell Avatar
    Phil Stilwell

    Steve, thanks for jumping in. You’re absolutely right to bring up the odds form of Bayes’ Theorem—it’s a valid and powerful tool. But the issue isn’t with the formula. It’s with the missing input. Specifically: apologists often never assign a resurrection probability at all. That’s not a small oversight—it’s a dealbreaker.

    1. Bayes Requires a Resurrection Prior—But It’s Always Missing

    You point out that likelihoods can outweigh priors. True—but only after the priors are defined. What is the actual prior probability of a resurrection? If that value isn’t explicitly stated and justified, then saying the resurrection is “the most probable explanation” is meaningless. The engine can’t run if a critical variable is left blank.

    2. Inflating the Likelihood Ratio Doesn’t Excuse a Missing Prior

    You highlight that the evidence (empty tomb, postmortem appearances, etc.) is far more likely under the resurrection hypothesis than under naturalistic ones. Even if we grant that—and it’s a big if—it still doesn’t salvage the argument unless the prior is specified. You can’t multiply a likelihood by an undefined prior and pretend it yields a reliable result.

    3. The Resurrection Is Often Given an Implied Default of 1% or More—Without Justification

    In practice, many apologists treat the resurrection hypothesis as though it starts with a reasonable prior—1%, 5%, sometimes more. But nothing in our background knowledge of the world justifies assigning such numbers. This is where the asymmetry becomes stark: naturalistic explanations, even when assigned extremely low priors (e.g. 0.1% each), are still actually assigned values and summed disjunctively. The resurrection hypothesis often gets a rhetorical pass.

    4. The Burden of Quantification Is on the Extraordinary Claim

    Bayesian reasoning isn’t magic. It can’t rescue a claim whose prior hasn’t been defended. Until apologists are willing to say what they think the prior probability of a resurrection is—and why—then all downstream comparisons are epistemically hollow. They’re trying to win a probability contest without submitting a number.

    Bottom Line: No Prior = No Probability Claim

    If someone claims “the resurrection is the most probable explanation,” they are making a comparative assertion. And no comparative claim is valid if one of the terms is left undefined. Until the resurrection’s prior is named, supported, and compared against the disjunction of natural alternatives, the argument doesn’t merely fall short—it never begins.

    I appreciate your attempt to incorporate Bayesian reasoning here. But your central claim—that the “likelihood can outweigh the prior”—only holds after a prior is actually specified. Right now, that key term is being left blank, and without it, any posterior probability is floating in the void.

    You’re essentially saying:

    “Even if the resurrection is unlikely to begin with, the specific evidence is so much more expected if the resurrection happened than if it didn’t, that this makes the resurrection probable overall.”

    That can work in Bayesian reasoning—but only when all the terms are assigned values.

    Let me ask directly:
    What do you assign as the prior probability of a resurrection?
    If you don’t provide that, there’s no way to judge whether the likelihood ratio “outweighs” it.

    More importantly, even if the evidence (e.g., empty tomb, postmortem experiences) is very unlikely under individual natural explanations, the combined disjunction of all natural alternatives—even at small individual probabilities—can still easily exceed the resurrection hypothesis, especially if no coherent prior is given for it.

    So yes, LP can shift things—but only if PP is present in the equation. Right now, resurrection arguments often assume the LP speaks for itself and quietly smuggle in a favorable prior without ever justifying it. That’s not Bayesian reasoning. That’s Bayesian aesthetics.

    Reply

Leave a comment

Recent posts

  • ✓ The Semantic Creep of Faith

    Hebrews 11:1 is often misquoted as a clear definition of faith, but its Greek origins reveal ambiguity. Different interpretations exist, leading to confusion in Christian discourse. Faith is described both as assurance and as evidence, contributing to semantic sloppiness. Consequently, discussions about faith lack clarity and rigor, oscillating between certitude…

  • ✓ AI for Christian Apologists

    This post emphasizes the importance of using AI as a tool for Christian apologetics rather than a replacement for personal discernment. It addresses common concerns among Christians about AI, advocating for its responsible application in improving reasoning, clarity, and theological accuracy. The article outlines various use cases for AI, such…

  • ✓ Deductive Closure on Inductive Contingencies

    This post argues that if deductive proofs demonstrate the logical incoherence of Christianity’s core teachings, then inductive arguments supporting it lose their evidential strength. Inductive reasoning relies on hypotheses that are logically possible; if a claim-set collapses into contradiction, evidence cannot confirm it. Instead, it may prompt revisions to attain…

  • ✓ A Typical Christian Post

    This post addresses common excuses for rejecting Christianity, arguing that they stem from the human heart’s resistance to surrendering pride and sin. The piece critiques various objections, such as the existence of multiple religions and perceived hypocrisy within Christianity. It emphasizes the uniqueness of Christianity, the importance of faith in…

  • ✓ Mistaking Structural Failure for Moral Fact

    The Outrage Trap discusses the frequent confusion between justice and morality in ethical discourse. It argues that feelings of moral outrage at injustice stem not from belief in objective moral facts but from a violation of social contracts that ensure safety and cooperation. The distinction between justice as a human…

  • ✓ Age of Accountability Calculus

    Isn’t the killing of infants always best under Christian theology? This post demonstrates that the theological premises used to defend biblical violence collapse into absurdity when applied consistently. If your theology implies that a school shooter is a more effective savior than a missionary, the error lies in the theology.

  • ✓ The Repellent Effect in Apologetics

    This article discusses the counterproductive nature of hostile Christian apologetics, which can inadvertently serve the skepticism community. When apologists exhibit traits like hostility and arrogance, they undermine their persuasive efforts and authenticity. This phenomenon, termed the Repellent Effect, suggests that such behavior diminishes the credibility of their arguments. As a…

  • ✓ Mental Irreductionism?

    The post argues against the irreducibility of conscious experiences to neural realizations by clarifying distinctions between experiences, their neural correlates, and descriptions of these relationships. It critiques the regression argument that infers E cannot equal N by demonstrating that distinguishing between representations and their references is trivial. The author emphasizes…

  • ✓ The Digital Berean

    The article highlights the value of AI tools, like Large Language Models, to “Red Team” apologetic arguments, ensuring intellectual integrity. It explains how AI can identify logical fallacies such as circular reasoning, strawman arguments, and tone issues, urging apologists to embrace critique for improved discourse. The author advocates for rigorous…

  • ✓ Differentiating Effects of the Spirit?

    The concept of the Holy Spirit’s indwelling is central to Christian belief, promising transformative experiences and divine insights. However, this article highlights that the claimed supernatural benefits, such as unique knowledge, innovation, accurate disaster predictions, and improved health outcomes, do not manifest in believers. Instead, evidence shows that Christians demonstrate…

  • ✓ The Source of Human Rights

    This post examines the widespread claim that human rights come from the God of the Bible. By comparing what universal rights would require with what biblical narratives actually depict, it shows that Scripture offers conditional privileges, not enduring rights. The article explains how universal rights emerged from human reason, shared…

  • ✓ The Evasion of 1 Samuel 15:3

    This post exposes how Christian apologists attempt to escape the moral weight of 1 Samuel 15:3, where God commands Saul to kill infants among the Amalekites. It argues that the “hyperbole defense” is self-refuting because softening the command proves its literal reading is indefensible and implies divine deception if exaggerated.…

  • ✓ Atrocity Blunders on Both Sides

    This post challenges both skeptics and Christians for abusing biblical atrocity texts by failing to distinguish between descriptive and prescriptive passages. Skeptics often cite descriptive narratives like Nahum 3:10 or Psalm 137:9 as if they were divine commands, committing a genre error that weakens their critique. Christians, on the other…

  • ✓ The Irrelevance of the Messenger

    In rational inquiry, the source of a message does not influence its validity; truth depends on logical structure and evidence. Human bias towards accepting or rejecting ideas based on origin—known as the genetic fallacy—hinders clear thinking. The merit of arguments lies in coherence and evidential strength, not in the messenger’s…

  • ✓ When Inerrancy Becomes Moot

    The defense of biblical inerrancy overlooks a critical flaw: internal contradictions within its concepts render the notion incoherent, regardless of textual accuracy. Examples include the contradiction between divine love and commanded genocide, free will versus foreordination, and the clash between faith and evidence. These logical inconsistencies negate the divine origin…

  • ✓ Apologists’ Favorite Arguments

    The referenced video outlines various arguments for the existence of God, categorized based on insights from over 100 Christian apologists. The arguments range from existential experiences and unique, less-cited claims, to evidence about Jesus, moral reasoning, and creation-related arguments. Key apologists emphasize different perspectives, with some arguing against a single…

  1. Phil Stilwell's avatar

    Ryan, your response attempts to bridge the gap between ancient text and modern rationality, but it relies on several logical…

  2. Ryan Stohldrier's avatar
  3. Ryan Stohldrier's avatar

    [Biblical faith, as presented in the New Testament, is primarily concerned with conviction in divine authority, rather than rational belief…

  4. Phil Stilwell's avatar
  5. J's avatar
  6. J's avatar
  7. J's avatar
  8. Phil Stilwell's avatar
  9. Ryan Stohldrier's avatar
  10. J.'s avatar

Phil Stilwell

A Deep Dive into Common Faith-Based Concepts & Claims

Free of Faith